浅谈通信系统的均衡准则与实现

一、均衡的概念

二、均衡器的作用：校正或补偿系统特性，减小码间串扰的影响！

均衡器在系统中的位置：

三、均衡的分类：

一般情况下，频域均衡器很难实现，现实或研究中，均衡一般都是指时域均衡器

下图是一个横向滤波器的时域均衡系统：

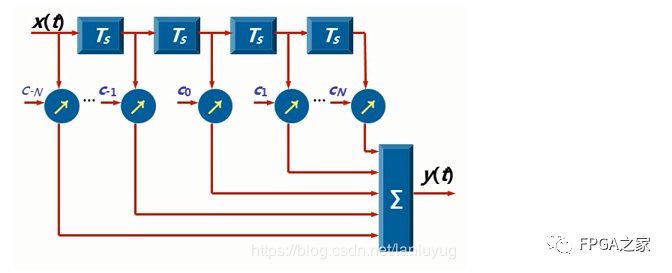
下面波形图中，均衡的目标是使上面的波形补偿至下端的波形图，即将不为0时刻的采样点都补偿至0，对应克表示为右边的公式。

下面有一各均衡器的一个三抽头的横向滤波器的习题例子：

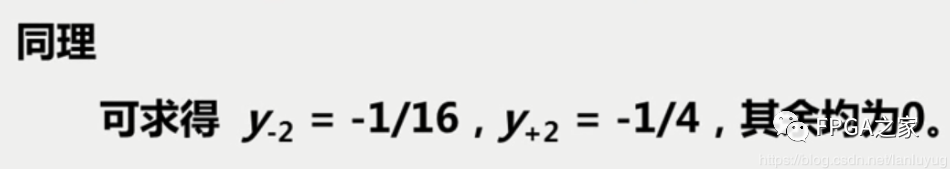
二、均衡准则与实现

问题：如何调整抽头系数以获取最佳均衡效果？

有以下一些准则：

1. 峰值失真（准则）：

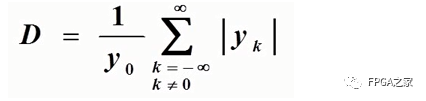
物理意义：所有抽象时刻的码间串扰绝对值之和与t=0时刻的抽样值之比，即峰值码间干扰与有用信号的样值之比。

最佳均衡则使峰值失真D最小化。

2. 均方失真（准则）

即峰值码间干扰的平方与有用信号的各样值平方求和之比，就是在峰值失真各项加上平方。

最佳均衡则使均方失真D最小化。

最小峰值失真准则的工作原理：迫零均衡

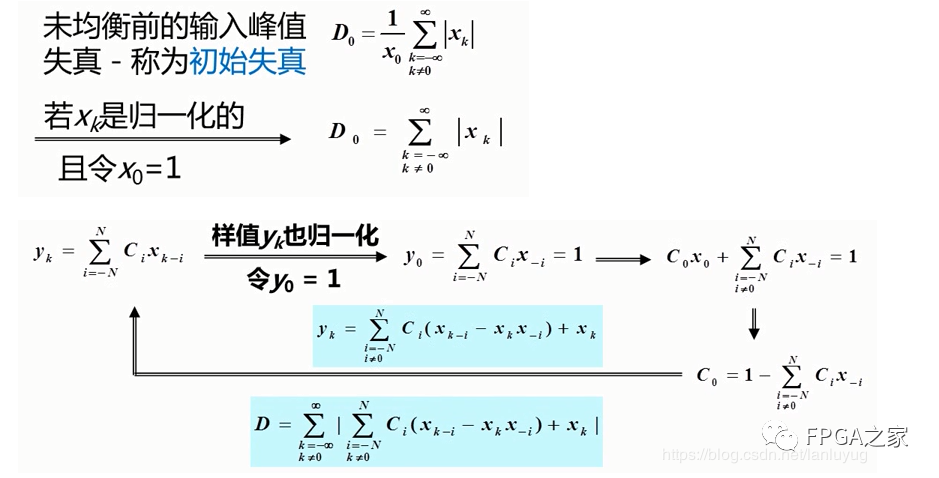
上面的迫零是使D的值最小；

下面Lucky的证明比较重要：

上面定理的数学意义是：系数{Ci}应该是下式：

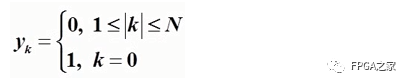
成立时的2N+1个联立方程的解。这2N+1个线性方程为：

来看看Lucky发明的原始的迫零均衡器：

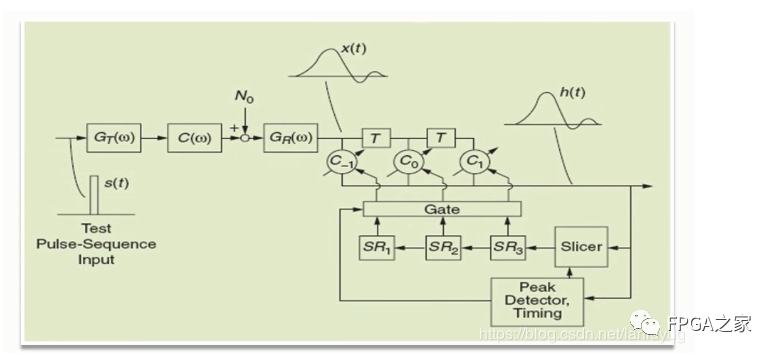
上面这个原始的迫零均衡器，在其前面设置了一个测试脉冲序列，也就是一个已知的序列对抽头系数进行与训练，后面Lucky又发明了一个自适应的均衡器。

再来看个迫零均衡器的习题吧：

结论：抽头有限时，不能完全消除码间干扰，但是适当增加抽头数可以将码间串扰减小到相当小的程度。

均衡器的实现与调整，如下所示，均衡器主要研究的是自动均衡器，而自动均衡器又分为较为原始的预置式均衡器和自适应均衡器。

最重要的应用来了，上述经典的自适应均衡算法，都属于线性均衡器，如果像电话线这样的信道来说，性能还是非常好的。

有线传输的信道来说，常用的信道均衡算法（线性均衡器）有：迫零算法（ZF）；最小均方误差算法（LMS）；递推最小二乘算法(RLS);卡尔曼算法等。

无线信道均衡算法（非线性均衡器）：判决反馈均衡（DFE）、最大似然符号检测、最大似然序列估值。

来看看发展吧：

编辑：黄飞