时间:2018-09-17 07:57
人气:
作者:admin
摘要
在区块链中,不同节点为了达成数据一致而按照同一套逻辑处理数据。但有时候,区块链节点可能为了自身利益而发送错误的信息,也有可能因为网络中断而无法传递接收信息,这就使区块链网络中的节点得到不一致的结果,从而破坏系统一致性。拜占庭将军问题被认为是在分布式系统中达成共识的最难解的问题之一,而与之对应的拜占庭容错共识算法是区块链网络的基础设施之一。
1982年,图灵奖获得者莱斯利 · 兰伯特(Leslie Lamport)发表了一篇重要的论文《拜占庭将军问题》(The Byzantine Generals Problem),由此展开了长达几十年的、关于如何在分布式系统中有节点被故意破坏的情况下达成共识的讨论。
随着区块链技术的出现,这种讨论有愈演愈烈的趋势。但对大多数人来说,直接去啃论文,无异于望梅止渴,并不能很好地理解论文中要表达的思想。在这篇文章里,我就带你通俗地学习拜占庭将军问题背后的共识协议。
两个将军问题
首先我们来看一个比较简单的例子,我们姑且就称之为“两个将军问题”吧,情形是这样的:
有两支军队一起攻打一座城市,他们各自由一名将军领导。两支军队各自占领城市附近两个不同的山谷。两军之间隔着一个山谷,双方间唯一的通信方式就是派遣信使来往于三个山谷。不幸的是,中间山谷已被城市保卫军占领,也就意味着:信使在通过山谷时可能会被捕。
现在两支军队要协商进攻城市的时间,因为只有两支军队一起进攻才能获得战斗的胜利。所以他们就必须沟通一个时间点来发起进攻,并同意就在那时发动攻击。大家可以想一想,两位将军能就何时进攻达成一致么?
A1和A2军队需要协调,但是他们派出的信使有可能被B军队拦截
现在,我来展开介绍这个过程。
A1将军写了封进攻信“我们两支军队凌晨四点一起发动总攻”,并将信交给信使。信使将信带出去后,A1将军根本不知道信使是被捕了还是已将信送达。因此,A1将军会犹豫是否发动进攻,除非收到了A2将军的确认回信。
假设信使通过了山谷,将信交给了A2将军,A2将军写了封回信“我同意在凌晨四点发动总攻”,他将回信交给信使之后,A2将军也不知道信使是否成功将回信交给了A1将军。因此,A2将军会犹豫是否发动进攻,除非收到了A1将军的确认回信。
假设信使又成功地通过了封锁,将A2将军的确认进攻回信交给了A1将军。为了让A2将军放心,A1将军还得给A2将军写封信“我已经收到了你的确认,我们会取得胜利的”。但是,如果这次的信使被捕了呢?是否A2将军还得给A1将军发信“我确认我已经收到了你的确认消息”?
...
于是,你会发现两位将军陷入了僵局,因为他们不能确认信使是否将信息传递给了对方。因此,这个问题是无解的。
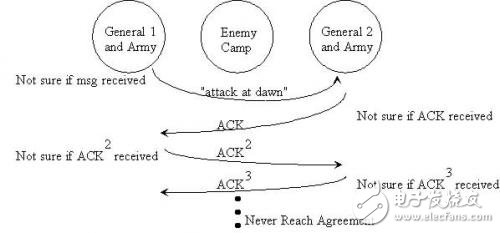
无限次重试,永远不可能达成共识
还有另外一个例子,是说三个人在不同房间,进行投票的故事。三个人彼此可以通过电话进行沟通,但经常会有人不接电话。比如某个时候,A 投票“赞成”,B 投票“反对”,但是C不接电话。A 和 B 永远无法在有限时间内获知最终的结果。如果可以重新投票,类似情形也同样会再次发生。
这背后其实有一个很著名的定理:“FLP不可能性”,它是指在分布式异步通信中,没有任何算法能保证一致性。
我们可能会觉得不可思议,因为在现在的软件系统架构中,分布式架构随处可见,比如Paxos算法。这里的区别在于FLP定理是学术定理,是遵循严格数学证明的,考虑的是最极端的情况,而Paxos算法是工程实践,学术上的极端性一般情况下很少发生,即便发生,多试几次可能就成功了。
正如第一个例子所示,不可能每次派出的信使都被B军队拦截,所以A1、A2将军可以一次性派出100个信使,只要有1个信使通过了封锁,就算是送信成功。而同样在投票的例子里,ABC每轮都给彼此打多次电话,直至打通,这样也能达成共识。
有句话是这么说的: 科学告诉你什么是不可能的;工程则告诉你,付出一些代价,我可以把它变成可能。这就是工程的魅力。 我很赞同。