固定增益运算放大器简化滤波器的设计-Fixed-Gai

Abstract: Use less component count, money, and board space when designing Sallen-Key filters. Simplify band pass filters with fixed gain amplfiers.

Simple second-order filters meet many filtering requirements. A low-order low-pass filter, for example, is often adequate for antialiasing in ADC applications or for eliminating high-frequency noise in audio applications. Similarly, a low-order high-pass filter can easily remove power-supply noise. When you design such filters with built-in gain, fixed-gain op amps can save space, cost, and time. Figure 1 illustrates the use of fixed-gain op amps in building second-order low-pass and high-pass Sallen-Key filters. Filter "cookbooks" are useful in designing these filters, but the cookbook procedures usually break down for a given response, such as Butterworth, if the gain set by RF and RG is greater than unity. What's more, the cookbook component-value formulas can yield unrealistic values for the capacitors and the resistors.


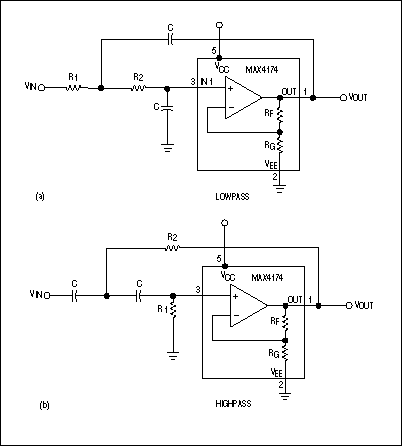
Figure 1. Sallen-Key filters use fixed-gain op amps to realize a second-order Butterworth response.

Butterworth filters, for example, offer the flattest passband. They also provide a fast initial falloff and reasonable overshoot. You can easily design such filters using the table below with the following equations: R2 = 1/(2πfC √) and R1 = XR2.

Butterworth-Filter-Design Criteria

Gain	Low-Pass X	High-Pass X
1.25	*	1.372
1.5	2	1.072
2	0.5	0.764
2.25	0.404	0.672
2.5	0.343	0.602
3	0.268	0.5
3.5	0.222	0.429
4	0.191	0.377
5	0.15	0.305
6	0.125	0.257
7	0.107	0.222
9	0.084	0.176
10	0.076	0.159
11	0.07	0.146
13.5	0.057	0.121
16	0.049	0.103
21	0.038	0.08
25	0.032	0.068
26	0.031	0.066
31	0.026	0.056
41	0.02	0.043
50	0.017	0.035
51	0.017	0.035
61	0.014	0.029
81	0.011	0.022
100	0.009	0.018
101	0.009	0.018

*A gain of 1.25 is impossible to obtain with matched capacitors for the low-pass case.

For a gained filter response, the use of a fixed-gain op amp reduces cost and component count. It also decreases sensitivity, because the internal, factory-trimmed, precision gain-setting resistors provide 0.1% gain accuracy. To design a second-order Butterworth low-pass or high-pass filter using a fixed-gain op amp, follow these steps:

1. Determine the corner frequency fC.
2. Select a value for C.
3. For the desired gain value, locate X under the proper column heading in the table.
4. Calculate R1 and R2 using the equations.

Choosing C and then solving for R1 and R2 lets you optimize the filter response by selecting component values as close to the calculated values as possible. C can be lower than 1000pF for most corner frequencies and gains. Fixed-gain op amps come optimally compensated for each gain version and provide exceptional gain-bandwidth products for systems operating at high frequencies and high gain. Suppose, for example, you must design a low-pass filter with a 24kHz corner frequency and a gain of 10. Step 1 is complete (fC = 24kHz). Next, complete Step 2 by selecting a value for C, say, 470pF. In the table, note that X = 0.076 for a low-pass filter with a gain of 10. Substitute these values in the equations:

R2 = 1/(2π fC √) = 1/(2π × 24kHz × 470pF × √ ) = 51kΩ, and R1 = XR2 = 0.076 × 51kΩ = 3.9kΩ.

Figure 2. Using the circuit values in the text, a simulation of the circuit in Figure 1a produces this Butterworth response.

A similar version of this article appeared in the July 6, 2000 issue of EDN.