有限带宽信号采样和混叠的数学分析

引言

现代应用中经常要求对模拟信号采样，将其转换为数字信号，然后对其进行计算处理，最后再重建为模拟信号。本文所探讨研究的主要问题是如何采样和重建模拟信号，同时又保持原始信号的全部信息。

有限带宽信号

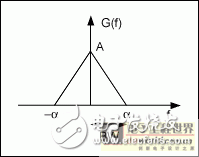
首先从有限带宽信号开始讨论。这样做取决于数学和物理两个方面的因素，下文将进行阐述。如果某个信号在某个频点(截止频率)以外的频谱幅度均为零，那么这一信号称为有限带宽信号。图1中的g(f)即是这样的信号，大于频点a的频率频谱幅度为零。在这种情况下，a也是这个基带信号的带宽(BW)。(由于频率为负没有物理意义，因此基带信号的带宽仅被定义为正频率。)

接下来对g(f)进行采样。我们可以利用数学形式表示该操作，即g(f)乘以一个时间间隔为T的冲激函数序列。通过将g(f)与冲激函数相乘，我们得到对应于冲激函数发生时刻的g(f)值，其它任何时间的乘积都为零。这类似于以fSAMPLING = 1/T的频率对g(f)采样。该操作可用公式1表示，采样后的新信号称为s(t)：

下一步是找出已采样信号s(t)的频谱。通过对公式1进行傅立叶变换可得到：

计算上面的积分比较复杂。为了简化计算，注意到s(t)是g(f)与冲激脉冲序列的乘积。同时我们还知道时域的乘法对应频域的卷积。(关于这一结论的证明可参考任何有关傅立叶变换的资料。) 因此，S(f)可以表示为：

注意公式3中的星号表示卷积，而不是相乘。我们已经知道原始信号的频谱g(f)，因此只需要算出冲激函数序列的傅立叶变换。我们知道冲激函数序列是一个周期函数，因而可以用傅立叶级数表示。如下式：

其中傅立叶系数为：

公式5中积分的上下限只指定为一个周期。当处理冲激函数时，这没有问题。然而，为了使上面的表达式具有更好的通用性，可以进行如下代换处理：用一个从负无穷到正无穷的傅立叶积分代替该积分，并用单个冲激函数―t周期信号的基本信号替代周期性的冲激函数序列。因而，公式5可以改写为：

这样一来冲激函数序列可采用以下易于进行傅立叶变换的简化表达式：

考虑到一个信号可以从其傅立叶变换积分得到，如下式：

并且：

最终表达式如下：

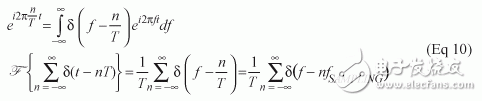
根据以上结果，再重新考虑已采样的基带信号。其傅立叶变换表达式如下：

两个信号A(f)和B(f)的卷积定义为：

则S(f)可表示为：

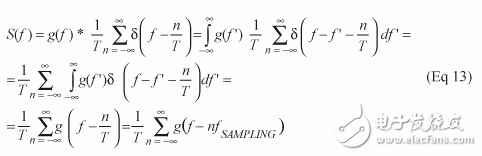
计算的结果为公式13，通常称为采样定理。它表明在时域里按周期T (秒)采样得到的信号会以1/T的频率重复原始信号的频谱，如图2所示。这一结果反过来可以清楚且直观地回答先前的问题：如何采样模拟信号才能够保持原始信号的全部信息？

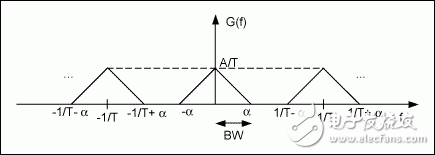
图2. 采样信号s(t)的频谱 

混叠效应

为保留原始基带信号的所有信息，必须确保每一个重复频谱“轮廓”之间不发生交叠。如果相互交叠(这种现象称为混叠)，就不可能再从采样信号中恢复出原始信号。这会使高频成分混叠到低频频段，如图3所示。

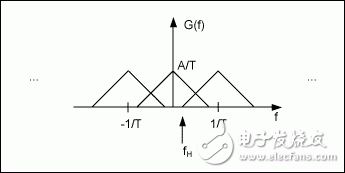
图3. 混叠对信号的影响