LabVIEW中集合的相关知识

从LabVIEW 2019开始推出了两种新的数据类型，分别是集合与映射表，它们都属于LabVIEW之前从未关注的一种数据类型—群体。NI介绍：群体是聚合同类数据的容器，群体中的每个对象为群体的元素或条目，使用群体数据类型创建用于存储和访问数据的高性能数据结构。由此可见群体数据类型类似于簇或数组，是存放简单数据类型的容器，同时它可以高效地存取数据。

本系列文章小编将介绍LabVIEW中的群体数据类型—集合与映射表，本篇文章为系列文章的第一篇—LabVIEW中的集合。下面请跟随小编一起来学习吧！

本文分享：

LabVIEW中的集合

一、 集合的概念

集合是一个数学概念，它是指具有某种特定性质的具体的或抽象的对象汇总而成的集体。其中，构成集合的这些对象称为该集合的元素，每一个元素仅在集合中出现一次，不会重复出现，换句话说就是集合中的元素是确定且唯一的。 在LabVIEW中，集合中的元素可以是任意基本数据类型（如数值、字符串、数组、簇等），LabVIEW中的集合是将相同类型的唯一有序数据元素归为一个集合。

二、 集合的API 生成集合：使用输入的所有元素创建一个集合。重复元素仅在结果集合中出现一次，每个输入的元素数据类型必须相同。

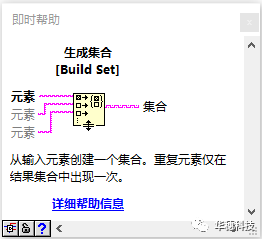
插入集合：给已有集合中插入一个新的元素后输出结果集合并返回该元素是否已包含在集合中，如果元素未包含在集合中则返回F，否则返回T。

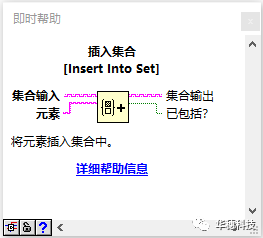
从集合中删除：从已有集合中删除指定元素后输出结果集合并返回该元素是否包含在集合中，如果元素包含在集合中则返回F，否则返回T。

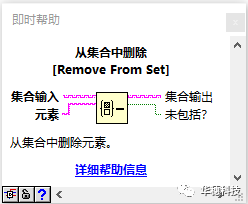
集合的元素？：查询输入的集合中是否包含输入元素，如果包含则返回T，如果不包含则返回F。

读取集合最大值和最小值：集合中的元素是唯一且确定的，同时它也是一个有序的，该API可以获取到一个集合中的最大元素和最小元素。

群体大小：返回输入的群体的元素个数，即群体的大小。（该API集合和映射表通用）

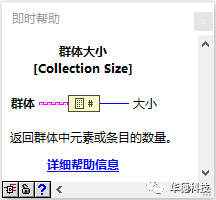
空群体：当输入的群体中元素个数为零时返回T。（该API集合和映射表通用）

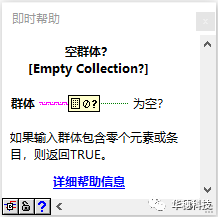
二、 集合的运算

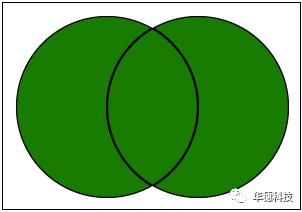
集合的并集：计算两个集合的并集，并集是属于任一集合的所有元素。

下图说明了此VI如何计算两个集合的并集。两个圆圈代表两个集合。绿色部分是并集。

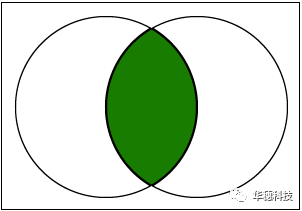
集合的交集：计算两个集合的交集。交集是属于两个集合的所有元素。

下图说明了此VI如何计算两个集合的交集。两个圆圈代表两个集合。绿色部分是交集。

集合的笛卡尔积：计算两个集合的笛卡尔积。笛卡尔积是一组两个元素的簇，涵盖了两个集合元素的所有可能组合。  

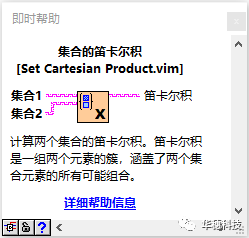
以下前面板演示了当集合1为{Down, Up}且集合2为{2, 3, 4}时，此VI如何计算笛卡尔积。  

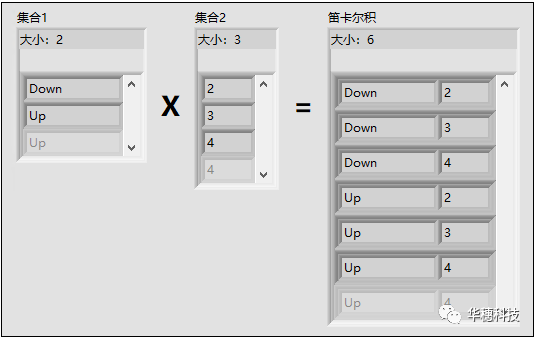
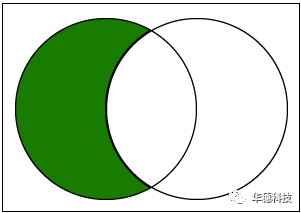
集合的差集：计算两个集合的差集。差集是第一个集合中包含但第二个集合中不包含的元素。

下图说明了此VI如何计算两个集合的差集。两个圆圈代表两个集合。绿色部分是差集。

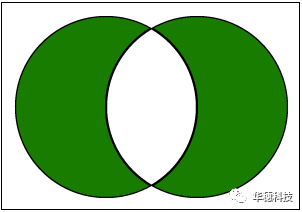
    集合的对称差：计算两个集合的对称差。对称差是两个集合的并集和交集的差集。

下图说明了此VI如何计算两个集合的对称差。两个圆圈代表两个集合。绿色部分是对称差。  

三、 集合的相关知识

1、由于集合按照有序顺序维护元素，相比未排序的数据结构（如数组），集合能够对数据进行更快地搜索、插入、更改及移除操作（集合操作数据的时间复杂度低于数组操作数据时的时间复杂度，所以效率较高），并且对于较大的数据同样适用。

2、集合按照有序顺序维护元素的操作将占用内存开销，数组不占用内存开销。

3、集合可以通过循环的索引输入访问到每个元素，并且再通过一次索引输出转换成一个数组，如下图所示：

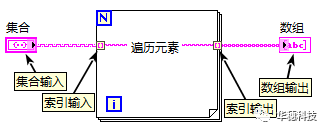
以上就是本篇关于LabVIEW中集合的所有内容啦。

编辑：黄飞