transformer原理解析

transformer架构可能看起来很恐怖，您也可能在YouTube或博客中看到了各种解释。但是，在我的博客中，我将通过提供一个全面的数学示例阐明它的原理。通过这样做，我希望简化对transformer架构的理解。 那就开始吧！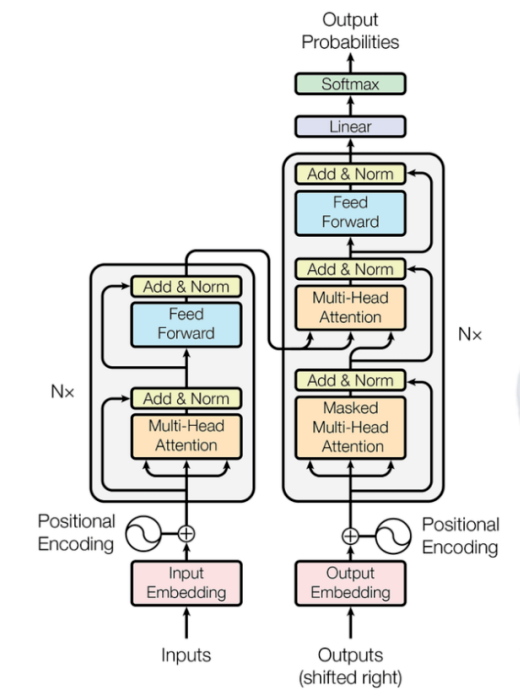

Inputs and Positional Encoding

让我们解决最初的部分，在那里我们将确定我们的输入并计算它们的位置编码。

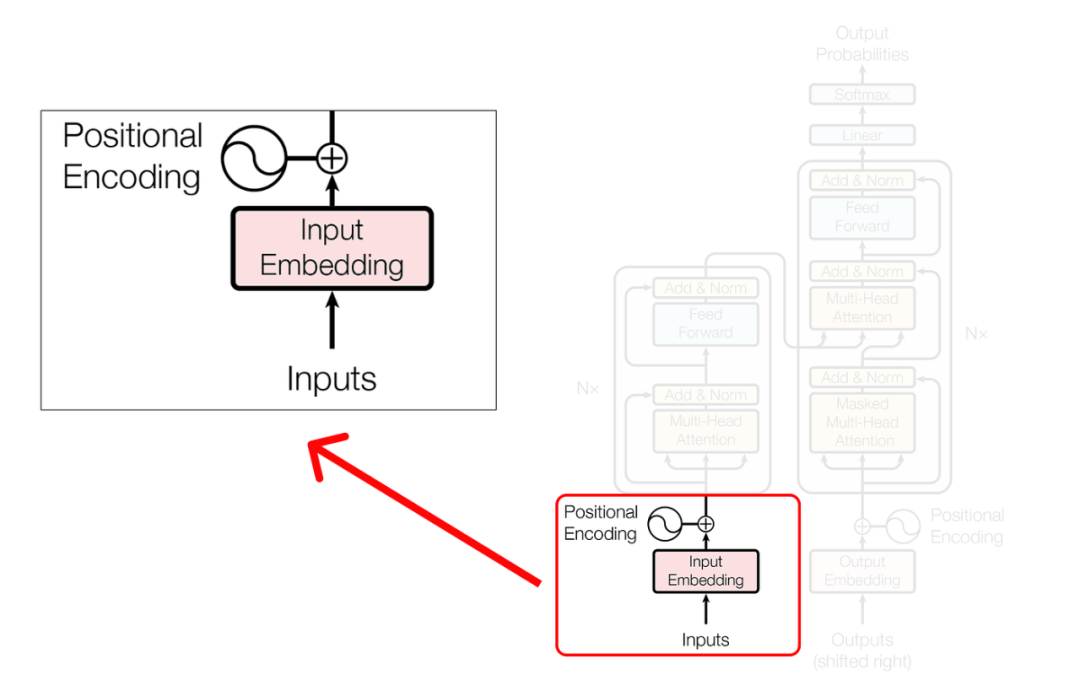
Step 1 (Defining the data)

第一步是定义我们的数据集(语料库)。

在我们的数据集中，有3个句子(对话) 取自《权力的游戏》电视剧。尽管这个数据集看起来很小，但它已经足以帮助我们理解之后的数学公式。

Step 2 (Finding the Vocab Size)

为了确定词汇量，我们需要确定数据集中的唯一单词总数。这对于编码(即将数据转换为数字) 至关重要。  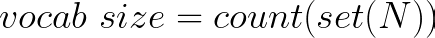 其中N是所有单词的列表，并且每个单词都是单个token，我们将把我们的数据集分解为一个token列表，表示为N。

获得token列表(表示为N) 后，我们可以应用公式来计算词汇量。 具体公式原理如下：

使用set操作有助于删除重复项，然后我们可以计算唯一的单词以确定词汇量。因此，词汇量为23，因为给定列表中有23个独特的单词。

Step 3 (Encoding and Embedding)

接下来为数据集的每个唯一单词分配一个整数作为编号。

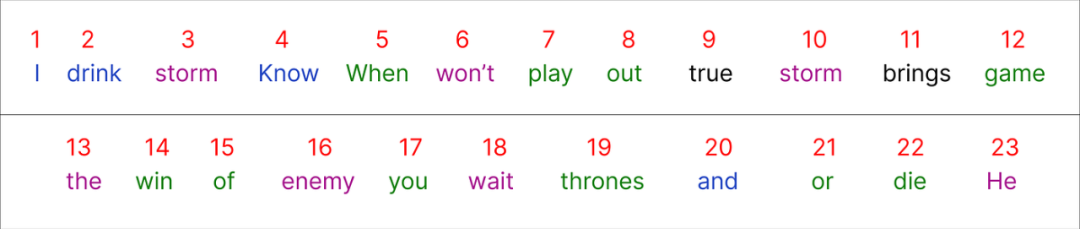
在对我们的整个数据集进行编码之后，是时候选择我们的输入了。我们将从语料库中选择一个句子以开始:   “When you play game of thrones”

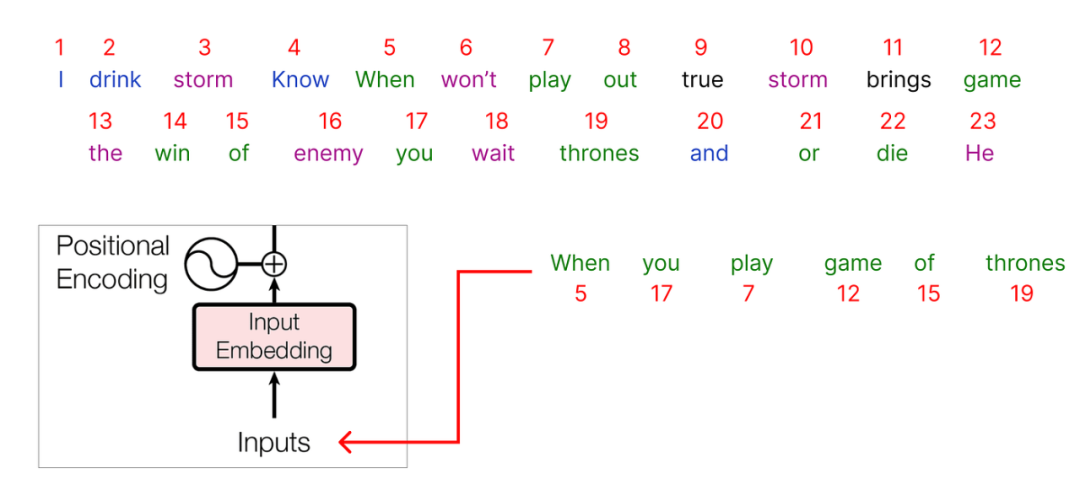
作为输入传递的每个字将被表示为一个编码，并且每个对应的整数值将有一个关联的embedding联系到它。

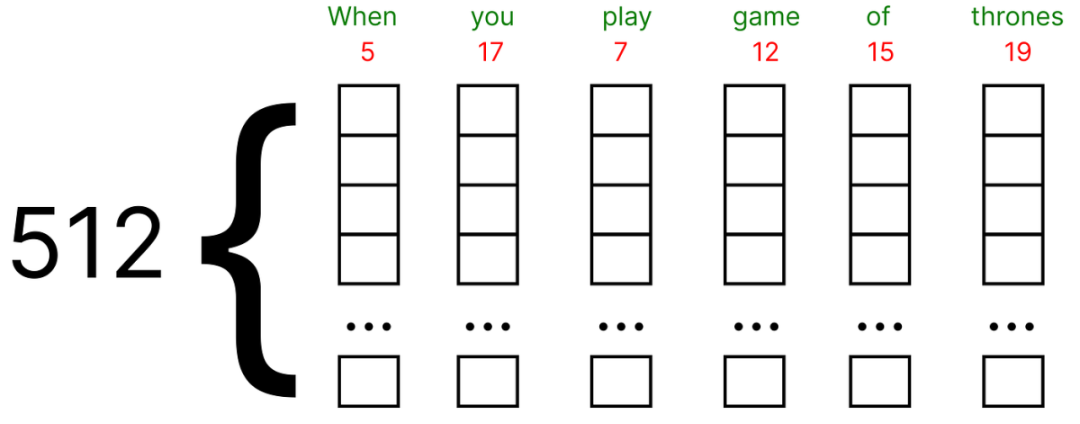
这些embedding可以使用谷歌Word2vec (单词的矢量表示) 找到。在我们的数值示例中，我们将假设每个单词的embedding向量填充有(0和1) 之间的随机值。

此外，原始论文使用embedding向量的512维度，我们将考虑一个非常小的维度，即5作为数值示例。

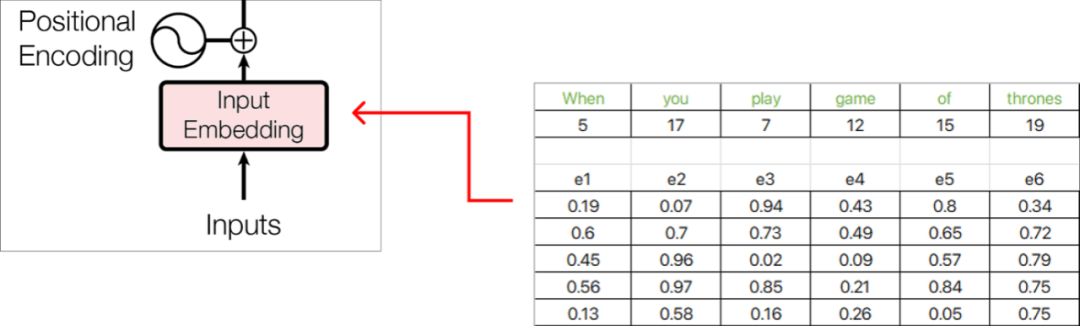
现在，每个单词embedding都由5维的embedding向量表示，并使用Excel函数RAND() 用随机数填充值。

Step 4 (Positional Embedding)

让我们考虑第一个单词，即“when”，并为其计算位置embedding向量。位置embedding有两个公式:

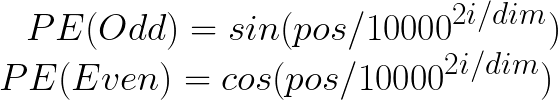
第一个单词“when”的POS值将为零，因为它对应于序列的起始索引。此外，i的值(取决于是偶数还是奇数) 决定了用于计算PE值的公式。维度值表示embedding向量的维度，在我们的情形下，它是5。

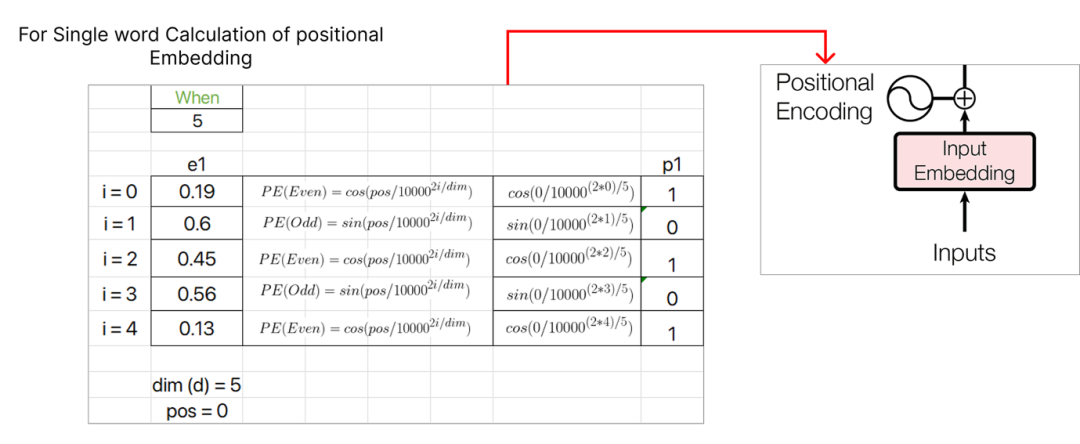
继续计算位置embedding，我们将为下一个单词“you” 分配pos值1，并继续为序列中的每个后续单词递增pos值。

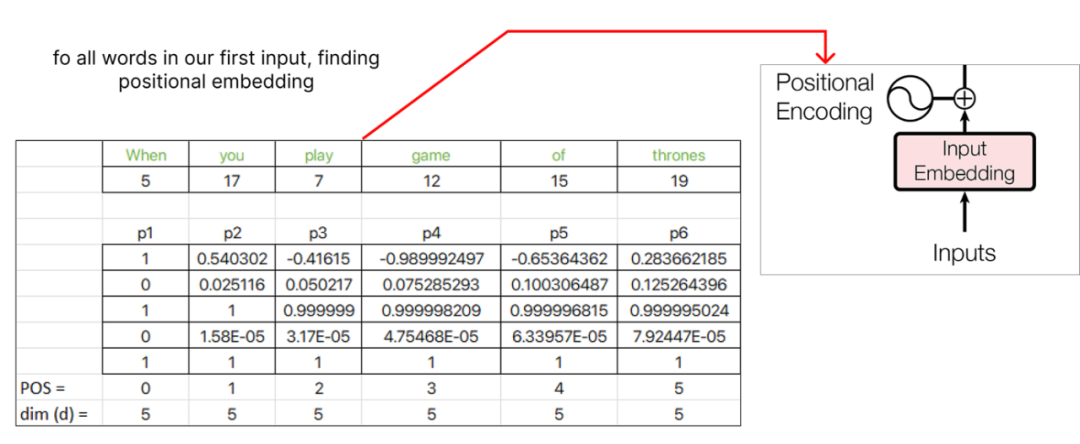
找到位置embedding后，我们可以将其与原始单词embedding联系起来。

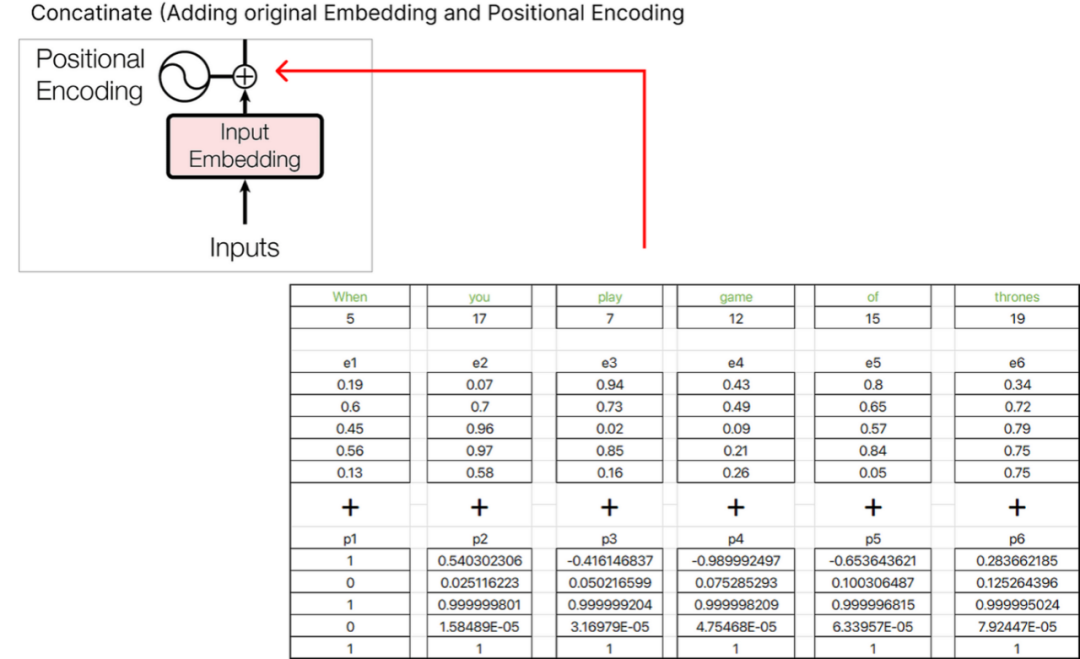
我们得到的结果向量是e1+p1，e2+p2，e3+p3等诸如此类的embedding和。  

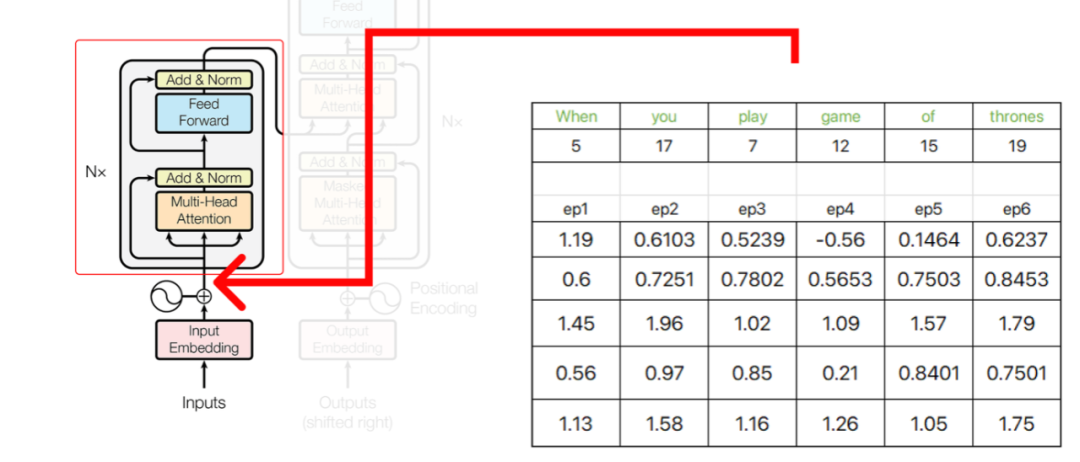
Transformer架构的初始部分的输出将在之后用作编码器的输入。  

编码器

在编码器中，我们执行复杂的操作，涉及查询（query），键（key）和值（value）的矩阵。这些操作对于转换输入数据和提取有意义的表示形式至关重要。

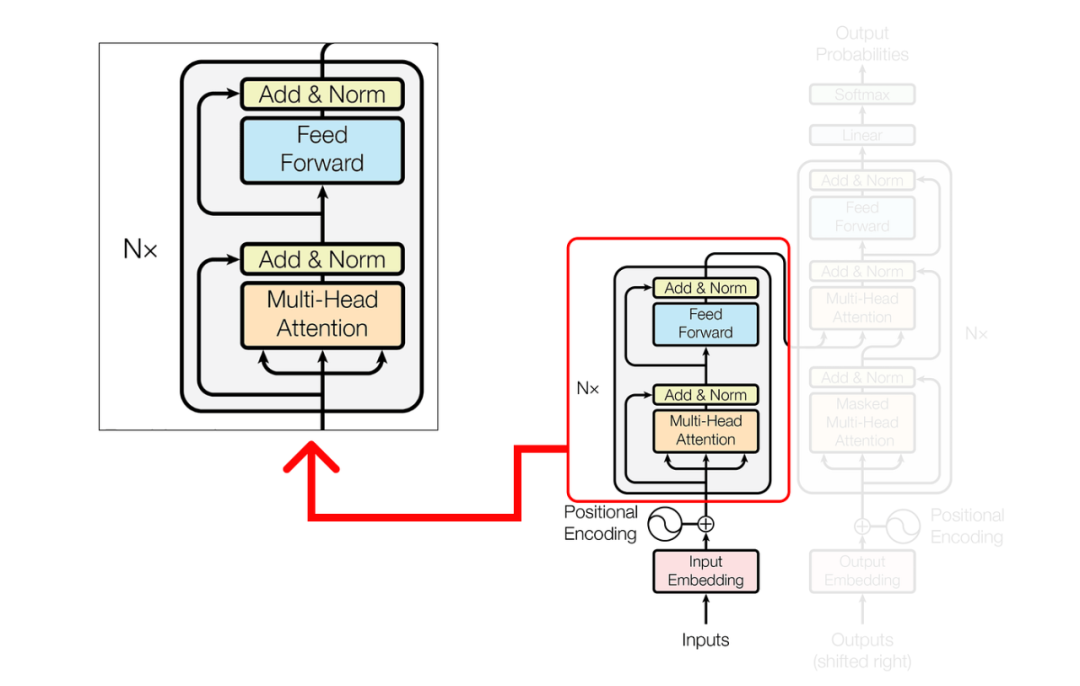
在多头注意力（multi-head attention）机制内部，单个注意层由几个关键组件组成。这些组件包括:

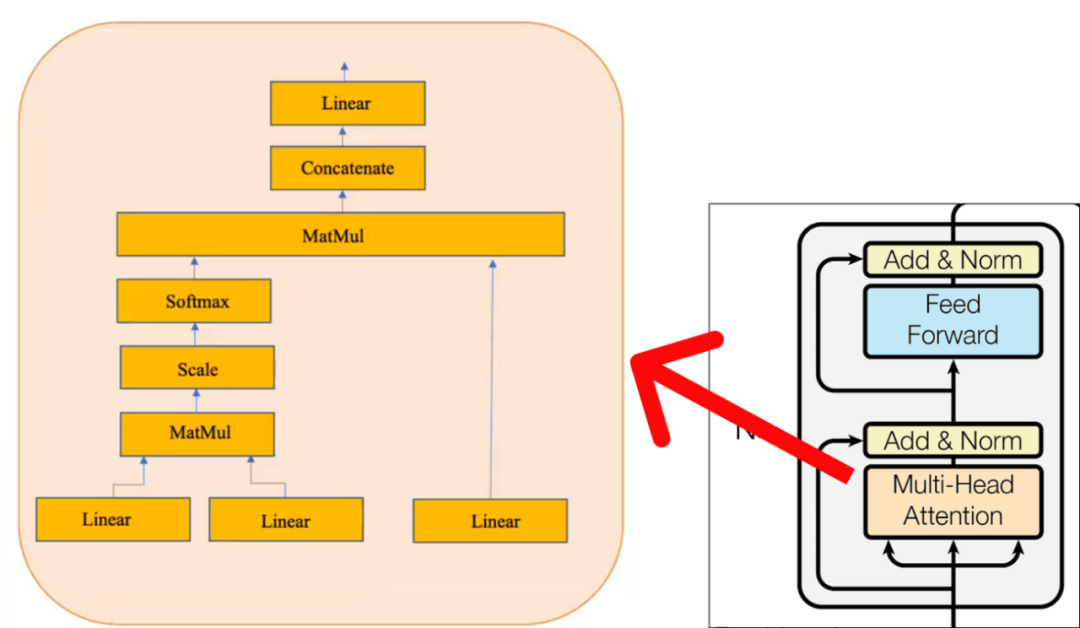
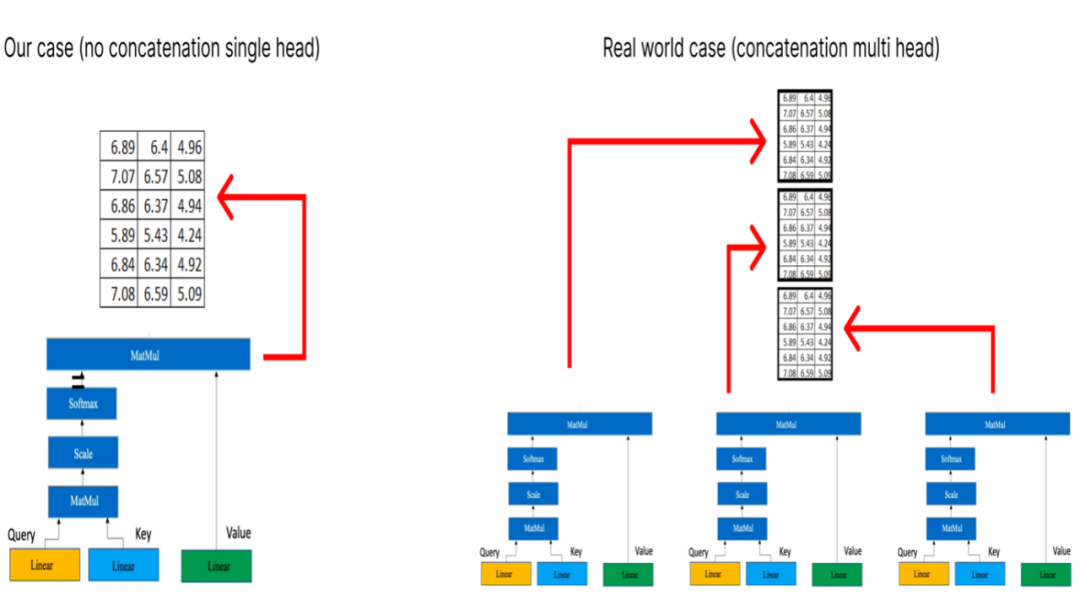
请注意，黄色框代表单头注意力机制。让它成为多头注意力机制的是多个黄色盒子的叠加。出于示例的考虑，我们将仅考虑一个单头注意力机制，如上图所示。

Step 1 (Performing Single Head Attention)

注意力层有三个输入

Query

Key

Value

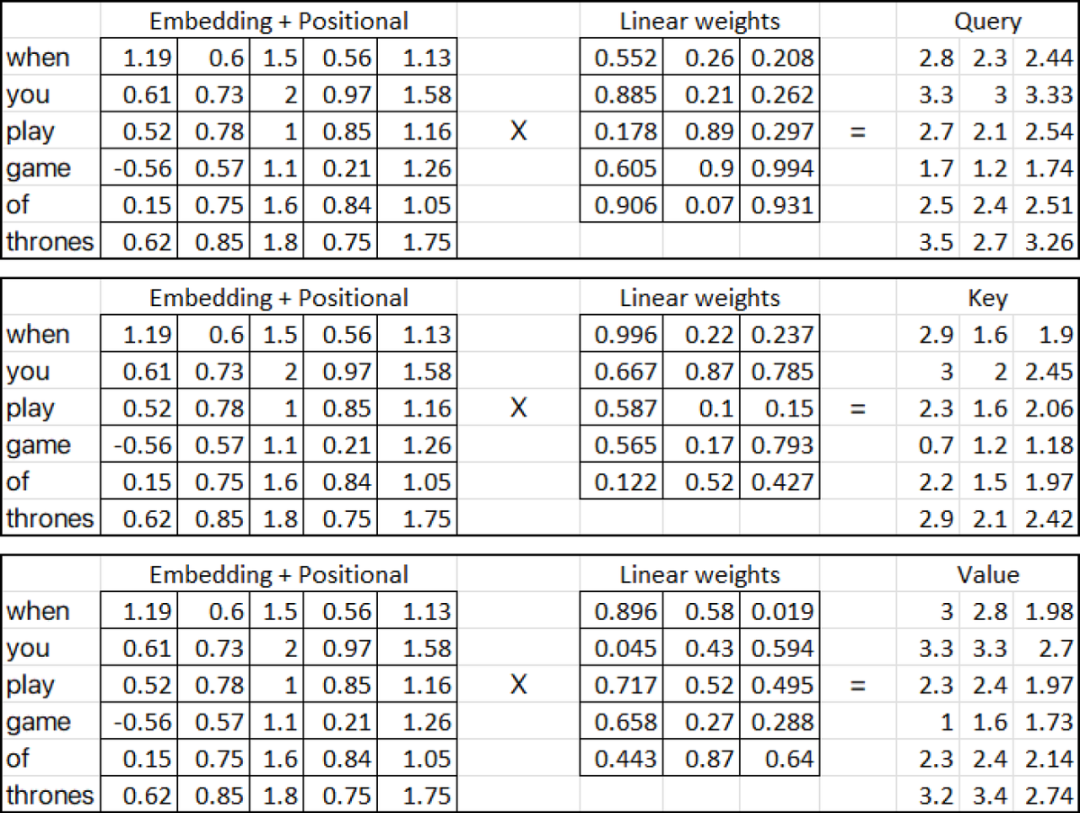
在上面提供的图中，三个输入矩阵(粉红色矩阵) 表示从将位置embedding添加到单词embedding矩阵的上一步获得的转置输出。另一方面，线性权重矩阵(黄色，蓝色和红色) 表示注意力机制中使用的权重。这些矩阵的列可以具有任意数量的维数，但是行数必须与用于乘法的输入矩阵中的列数相同。在我们的例子中，我们将假设线性矩阵(黄色，蓝色和红色) 包含随机权重。这些权重通常是随机初始化的，然后在训练过程中通过反向传播和梯度下降等技术进行调整。所以让我们计算(Query, Key and Value metrices):

一旦我们在注意力机制中有了query, key, 和value矩阵，我们就继续进行额外的矩阵乘法。

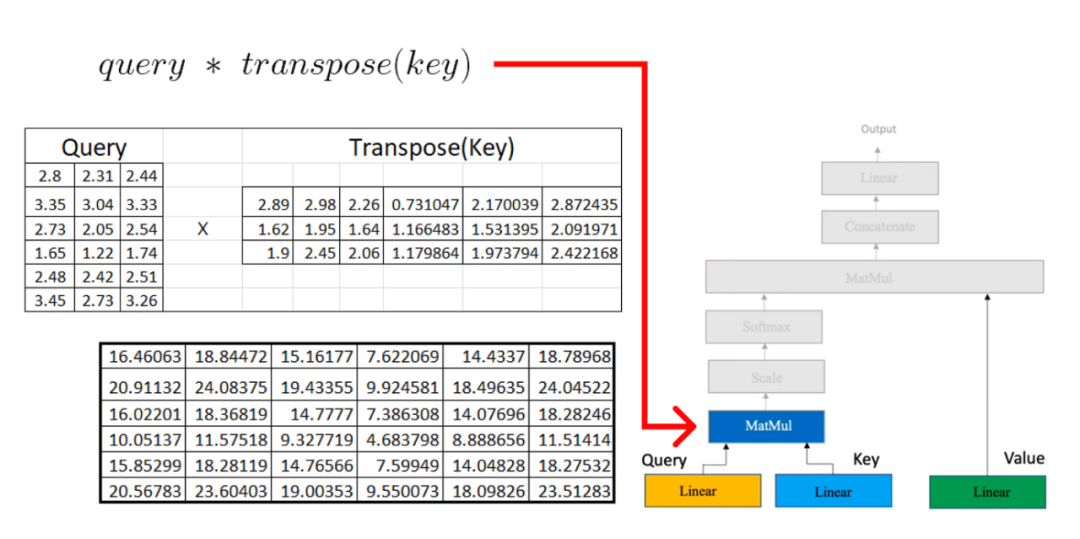
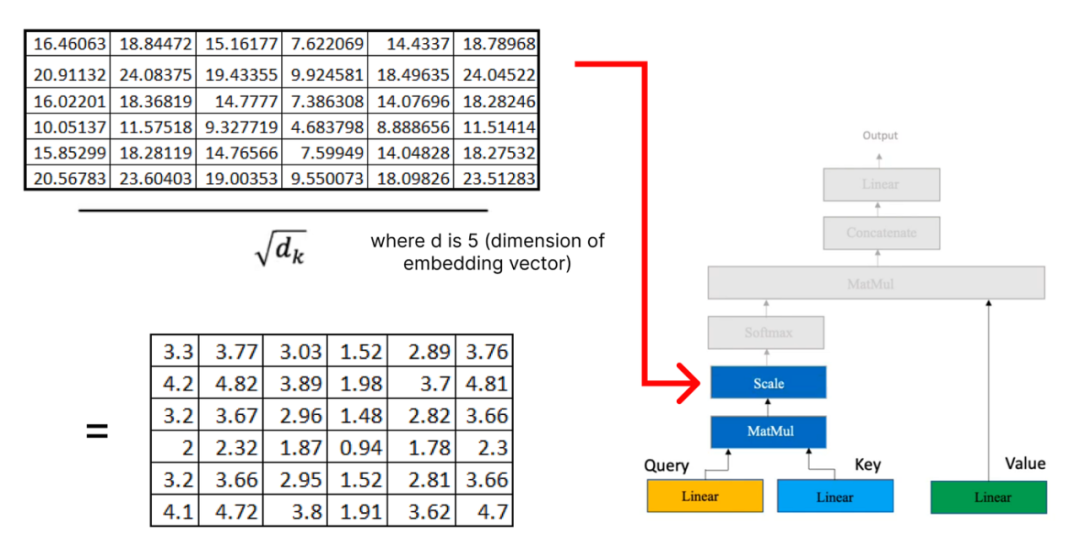
现在，我们将结果矩阵与我们之前计算的值矩阵相乘:

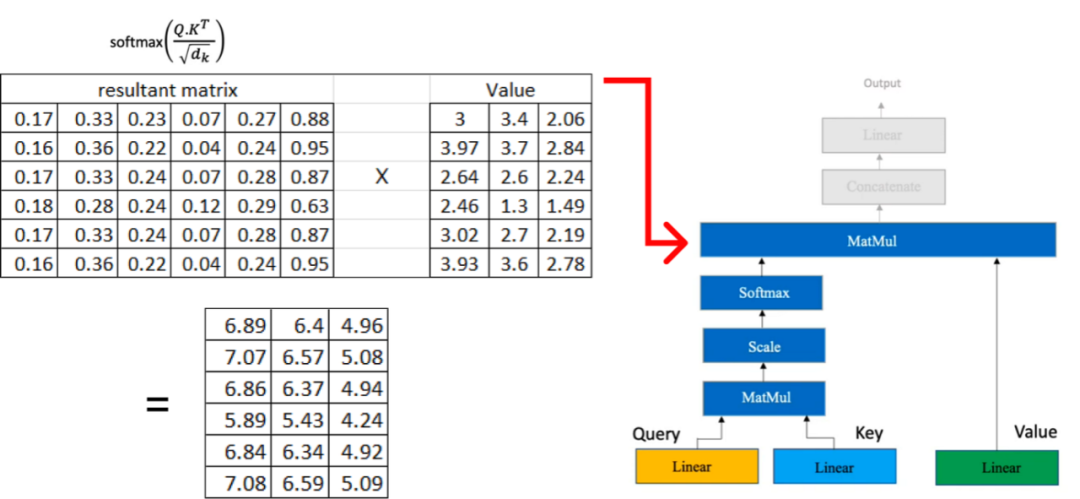
如果我们有多个头部注意力，每个注意力都会产生一个维度为(6x3) 的矩阵，那么下一步就是将这些矩阵级联在一起。

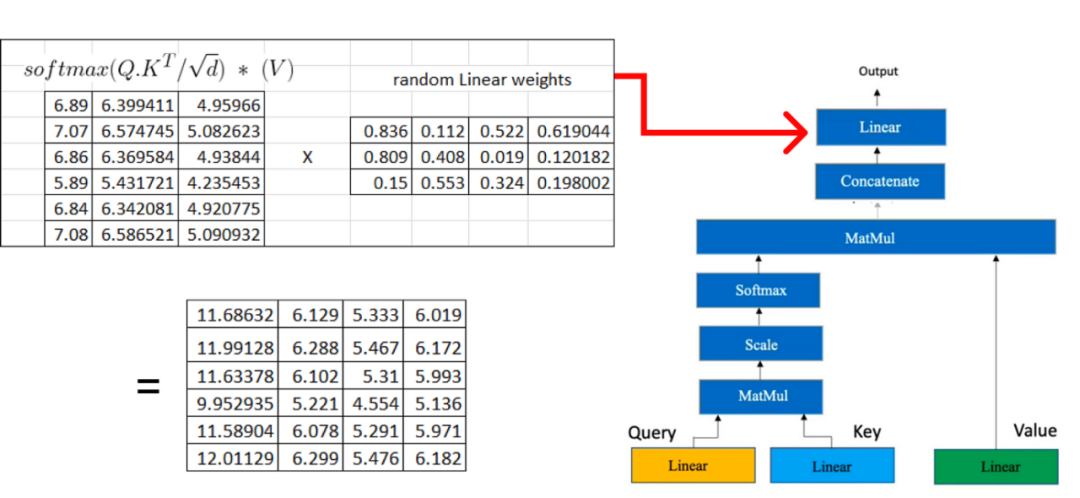
在下一步中，我们将再次执行类似于用于获取query, key, 和value矩阵的过程的线性转换。此线性变换应用于从多个头部注意获得的级联矩阵。

编辑：黄飞