什么是微分代数方程？Matlab求解微分代数方程

什么是微分代数方程？

微分代数方程是一类微分方程，其中一个或多个因变量导数未出现在方程中。方程中出现的未包含其导数的变量称为代数变量，代数变量的存在意味着不能将这些方程记为显式形式 y′=f(t,y)。

ode15s 和 ode23t 求解器可以使用奇异质量矩阵 M(t,y)y′=f(t,y) 来解算微分指数为1的线性隐式问题，包括以下形式的半显式 DAE

y′0=f(t,y,z)

0 =g(t,y,z)

在此形式中，由于主对角线存在一个或多个零值，因此代数变量的存在会产生奇异质量矩阵。

默认情况下，求解器会自动检验质量矩阵的奇异性，以检测 DAE 方程组。如果提前知道奇异性，则可将 odeset 的 MassSingular 选项设为 'yes'。对于 DAE，还可以使用 odeset 的 InitialSlope 属性为求解器提供 y′(0) 的初始条件估计值。

举个例子

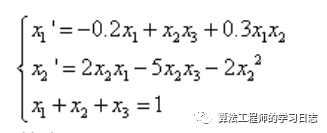
其中x1(0)=0.8;x2(0)=x3(0)=0.1;

1）方程写成DAE形式

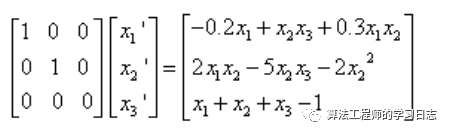
2）编程求解

%% 
clc
clear
close all
odefun = @(t,x)[-0.2*x(1)+x(2)*x(3)+0.3*x(1)*x(2);
                2*x(1)*x(2)-5*x(2)*x(3)-2*x(2)^2;
                x(1)+x(2)+x(3)-1]; %微分方程
M = [1 0 0;0 1 0;0 0 0]; % 质量矩阵
options=odeset('mass',M); % 定义mass属性
x0=[0.8;0.1;0.1];
[t,x]=ode15s(odefun,[0 10],x0,options);
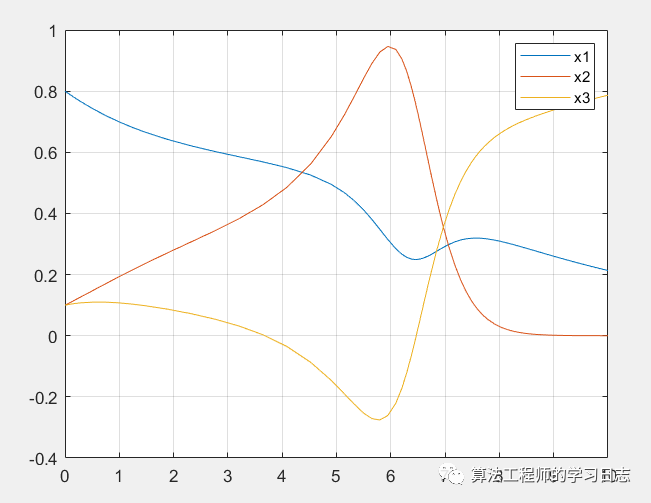
figure
plot(t,x(:,1),t,x(:,2),t,x(:,3))
grid on
legend('x1','x2','x3')