时间:2023-07-07 09:27
人气:
作者:admin
matlab数值计算与数值分析基础
MATLAB是一个功能强大的数值计算和科学计算软件,它提供了许多用于数值计算和数值分析的基础功能。下面是一些MATLAB中常用的数值计算和数值分析基础知识:
数值数据类型:MATLAB支持不同的数值数据类型,如整数(integers)、浮点数(floating-point numbers)和复数(complex numbers)等。
数值运算:MATLAB可以对数值进行基本的运算,包括加法、减法、乘法、除法、幂运算等。
数值数组:MATLAB通过矩阵和向量来处理数值数据。你可以使用MATLAB的数组操作符执行各种数学运算。
数值函数与库:MATLAB提供了许多内置的数值函数和数学库,如三角函数、指数函数、对数函数、特殊函数等。你可以直接调用这些函数进行数值计算。
数值求解:MATLAB提供了许多数值求解方法,例如求根(root finding)、插值(interpolation)、曲线拟合(curve fitting)和数值积分(numerical integration)等。
线性代数:MATLAB具有强大的线性代数功能,可以进行矩阵运算、线性方程组求解、特征值和特征向量计算等。
数值优化:MATLAB提供了优化工具箱,可以进行数值优化问题的求解,如最小化或最大化目标函数,并基于约束条件进行优化。
数值微分和积分:MATLAB提供了数值微分和积分函数,例如diff用于数值微分,integral用于数值积分。
数值方程求解:MATLAB提供了用于求解非线性方程、代数方程组和微分方程组等数值方程的函数,例如fsolve、solve和ode45等。
插值和拟合:MATLAB提供了插值函数和曲线拟合函数,如interp1用于一维插值,polyfit用于多项式拟合。
数值统计:MATLAB提供了用于数据分析和统计的函数,可以计算平均值、方差、标准差、相关系数等统计量。
随机数生成:MATLAB提供了各种分布的随机数生成函数,如均匀分布、正态分布、泊松分布等。
这些是MATLAB中数值计算和数值分析的一些基础知识和功能。通过灵活使用MATLAB的数值计算工具和函数,你可以解决各种数值计算问题,并进行数据分析、科学计算和工程计算等任务。在实践中,可以根据具体问题选择合适的工具和方法进行数值计算和分析。
示例演示
当涉及到MATLAB数值计算和数值分析时,下面是20个示例,涵盖了一些常见的用法:
数值积分:
integral(@(x)sin(x),0,pi)
数值微分:
diff(@(x)cos(x),0.5)
非线性方程求根:
fsolve(@(x)x^2-2,1.5)
线性方程组求解:
A=[1,2;3,4]; b=[5;6]; x=Ab;
曲线拟合:
x=linspace(0,2*pi,100); y=sin(x)+rand(size(x))*0.2; f=fit(x',y','sin1'); plot(f,x,y)
矩阵特征值和特征向量:
A=[1,2;3,4]; [eig_vec,eig_val]=eig(A);
傅里叶变换:
Fs=1000; t=0:1/Fs:1-1/Fs; x=sin(2*pi*50*t)+sin(2*pi*120*t); y=fft(x); f=(0:length(y)-1)*Fs/length(y); plot(f,abs(y))
信号滤波:
Fs=1000; t=0:1/Fs:1-1/Fs; x=sin(2*pi*50*t)+sin(2*pi*120*t); [b,a]=butter(3,[4555]/(Fs/2),'bandpass'); filtered_signal=filtfilt(b,a,x); plot(t,x,t,filtered_signal)
最小二乘拟合:
x=[1,2,3,4,5]; y=[1,3,6,10,15]; p=polyfit(x,y,2); f=polyval(p,x); plot(x,y,'o',x,f)
数值优化问题求解:
fun=@(x)x(1)^2+x(2)^2; x0=[1,1]; x=fminunc(fun,x0);
数值积分方程求解:
func=@(x)1./(1+x.^2); integral_value=integral(func,0,1);
插值:
x=[0,1,2,3]; y=[1,4,9,16]; xi=03; yi=interp1(x,y,xi); plot(x,y,'o',xi,yi)
求解常微分方程组:
func=@(t,y)[y(2);-y(1)]; [t,y]=ode45(func,[0,10],[1,0]); plot(t,y(:,1))
数值统计:
data=[1,2,3,4,5]; mean_value=mean(data); std_value=std(data);
随机数生成:
random_num=rand(1,10);
多项式求根:
coefficients=[1,-3,2]; roots_of_polynomial=roots(coefficients);
矩阵求逆:
A=[1,2;3,4]; inv_A=inv(A);
线性插值:
x=[0,1,2]; y=[1,3,2]; xi=02; yi=interp1(x,y,xi,'linear'); plot(x,y,'o',xi,yi)
蒙特卡洛方法:
count=0; n=100000; fori=1:n x=rand(); y=rand(); ifx^2+y^2<= 1 count = count + 1; end end pi_estimate = 4*count/n;
矩阵求秩:
A=[1,2;3,4]; rank_A=rank(A);
这些示例展示了MATLAB中数值计算和数值分析的一些常见用法。你可以通过这些示例来了解如何使用MATLAB进行数值计算和分析,并可根据具体需求进行进一步修改和调整。在实际应用中,可以根据具体问题选择合适的函数和方法进行数值计算和分析。
审核编辑:刘清
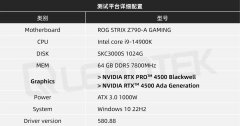
NVIDIA RTX PRO 4500 Blackwell GPU测试分析
