时间:2023-02-20 10:50
人气:
作者:admin
[导读] 前面分享了 IIR/FIR/mean/梳状数字滤波器的具体设计实现,这几种使用起来或许觉得计算量大,相对复杂。实际工程应用中通常有必要过滤来自传感器或音频流的数据,以抑制不必要的噪声。有的应用场景,可能只需要一个最简单的一阶滤波器即可。所以今天来分享一下怎么设计实现一阶数字滤波器。
小伙伴们一定都用过下面这个无源 RC 低通滤波电路:
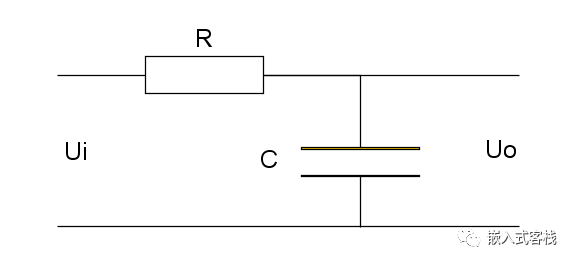 其拉普拉斯模型如下:
其拉普拉斯模型如下:
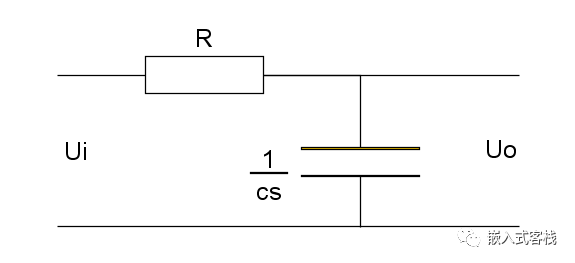 由于
由于
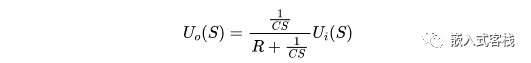
所以:
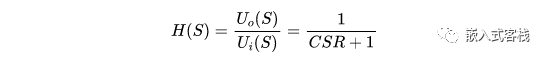
其幅频响应为:
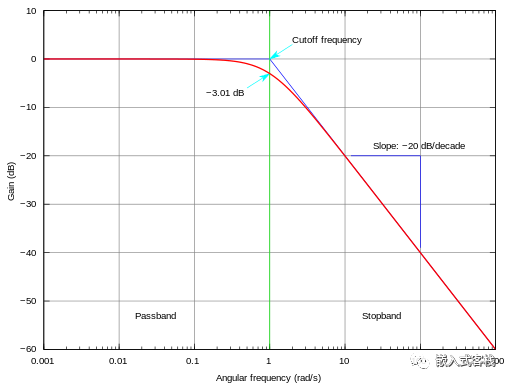
由其传递函数可知,这是一个单极点系统,其阻带满足-20dB/10 倍频程斜率下降。其截止频率为:
如把 C/R 交换位置则变成了高通滤波器,其截止频率依然按上式进行计算。这里也分享一个可在线计算的网址给大家:
http://www.elecfans.com/tools/rclvboqijiezhipinlv.html
其通带增益为 0dB。为什么要先谈谈硬件的一阶滤波器呢? 因为这个是大家最为熟悉的东西,而且也一定学过对其进行幅频响应分析。
既然硬件很容易实现一阶低通或者高通滤波器,那么为什么还要讨论一阶数字滤波器呢?
这里直接把差分方程列出来,具体推导就不罗嗦了,有兴趣可以找书看看,比较容易:
其中
表示滤波时间常数,T 表示采样周期。
clc;formatcompact
s=tf('s');
w=50;%rad/s
H=w/(s+w)
T=1/500;
Hd=c2d(H,T,'zoh')
opts=bodeoptions;
opts.FreqUnits='rad/s';
opts.XLim=[0.01,10000];
opts.Grid='on';
bode(H,Hd,opts)
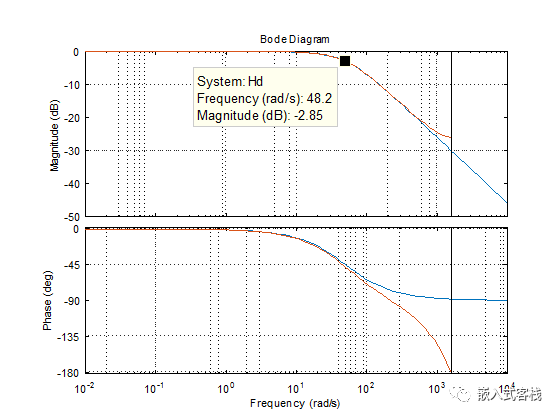
从其响应曲线看为一低通滤波器,相频响应不线性,从其差分方程也看出输出反馈参与运算了,所以其本质是 IIR 滤波器。
#include20*sin(2*PI*10*i/500)+rand()%5;
}
for(inti=0;ifprintf(pFile,"%f,%f
",sim[i],out[i]);
}
fclose(pFile);
return0;
}
取滤波时间常数为 0.005S,采样周期为 0.2S,为 40 倍关系,来看一下上述代码的滤波效果,波形未失真,效果棒棒哒~
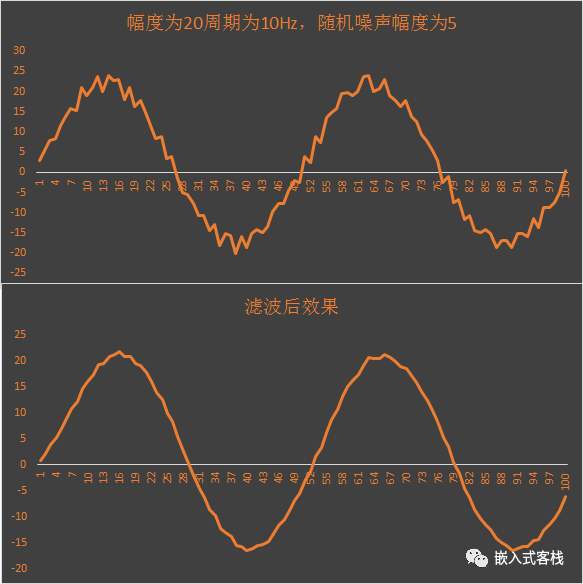
如果将常数修改为 0.1S,看下效果:
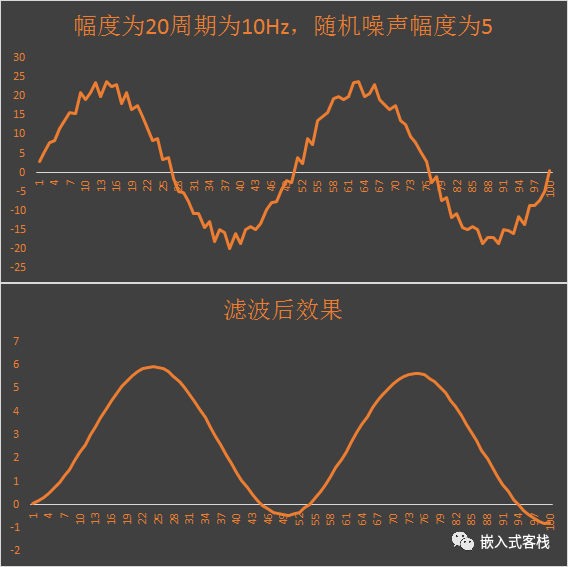
由图可见,幅度已经衰减,波形已经失真,传递函数的幅频响应已进入衰减区。所以实际使用的时候,滤波器时间常数尽量取小于采样周期 10 倍为宜,具体可以仿真一下,或者类似上面测试程序测试一下为宜。
一阶数字滤波计算简单,实现代价非常低。在滤除高频噪声时应用很广泛。其本质是 IIR 滤波器,为啥要单列出来介绍一下呢?是因为其实现简单,实际使用时也不必进行复杂的仿真。
审核编辑 :李倩
上一篇:APEX微技术SPICE模型
下一篇:单光子探测器研究现状与发展
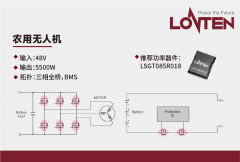
龙腾半导体SGT MOSFET LSGT085R018在智慧农业无