时间:2018-05-03 09:08
人气:
作者:admin
由于计算机视觉的大红大紫,二维卷积的用处范围最广。因此本文首先介绍二维卷积,之后再介绍一维卷积与三维卷积的具体流程,并描述其各自的具体应用。
1、二维卷积

• 图中的输入的数据维度为 14 × 14 ,过滤器大小为 5 × 5,二者做卷积,输出的数据维度为 10 × 10( 14 − 5 + 1 = 10 )。
• 上述内容没有引入channel的概念,也可以说channel的数量为1。如果将二维卷积中输入的channel的数量变为3,即输入的数据维度变为(14 × 14 × 3)。由于卷积操作中过滤器的 channel 数量必须与输入数据的channel数量相同,过滤器大小也变为 5 × 5 × 3 。在卷积的过程中,过滤器与数据在 channel 方向分别卷积,之后将卷积后的数值相加,即执行 10 × 10 次3个数值相加的操作,最终输出的数据维度为 10 × 10 。
• 以上都是在过滤器数量为1的情况下所进行的讨论。如果将过滤器的数量增加至16,即16个大小为10 × 10 × 3 的过滤器,最终输出的数据维度就变为10 × 10 × 16 。可以理解为分别执行每个过滤器的卷积操作,最后将每个卷积的输出在第三个维度(channel 维度)上进行拼接。
• 二维卷积常用于计算机视觉、图像处理领域。
2、一维卷积

• 图中的输入的数据维度为8,过滤器的维度为5。与二维卷积类似,卷积后输出的数据维度为8−5+1=48−5+1=4。
• 如果过滤器数量仍为1,输入数据的channel数量变为16,即输入数据维度为 8 × 16 。这里channel的概念相当于自然语言处理中的embedding,而该输入数据代表8个单词,其中每个单词的词向量维度大小为16。在这种情况下,过滤器的维度由5变为 5 × 16 ,最终输出的数据维度仍为 4 。
• 如果过滤器数量为 n,那么输出的数据维度就变为 4 × n。
• 一维卷积常用于序列模型,自然语言处理领域。
3、三维卷积
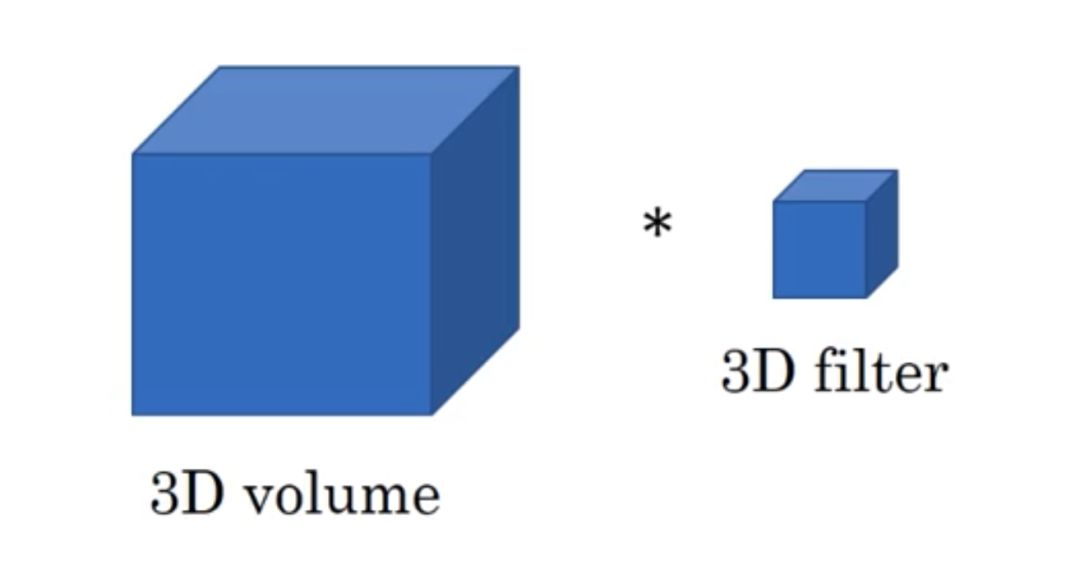
这里采用代数的方式对三维卷积进行介绍,具体思想与一维卷积、二维卷积相同。
• 假设输入数据的大小为 a1× a2× a3,channel数为 c,过滤器大小为f,即过滤器维度为 f × f × f × c(一般不写 channel 的维度),过滤器数量为 n。
• 基于上述情况,三维卷积最终的输出为 ( a1− f + 1 ) × ( a2− f + 1 ) × ( a3− f + 1 ) × n 。该公式对于一维卷积、二维卷积仍然有效,只有去掉不相干的输入数据维度就行。
• 三维卷积常用于医学领域(CT影响),视频处理领域(检测动作及人物行为)。
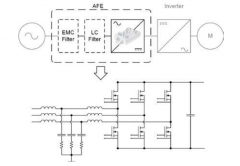
上一篇:分析一下转换器的技术规格及应用
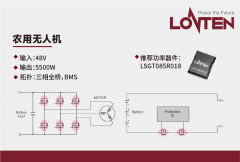
龙腾半导体SGT MOSFET LSGT085R018在智慧农业无