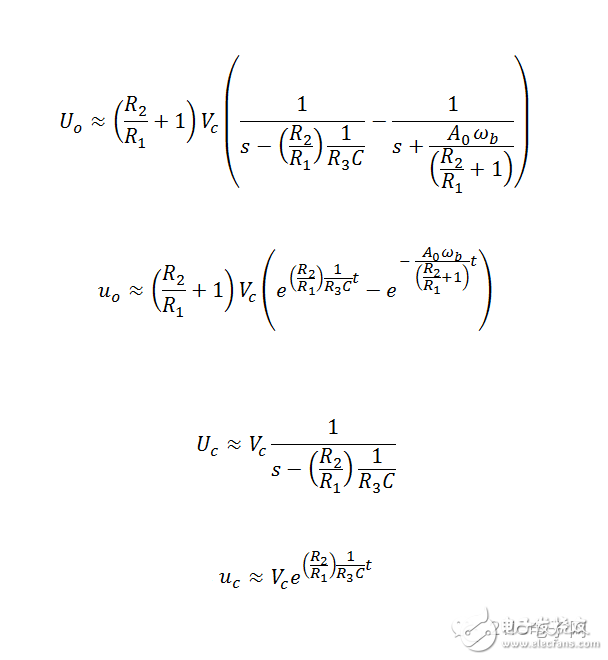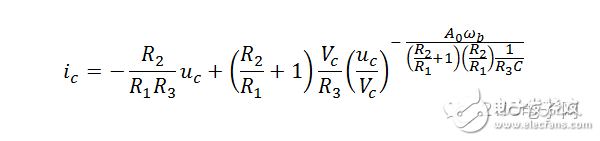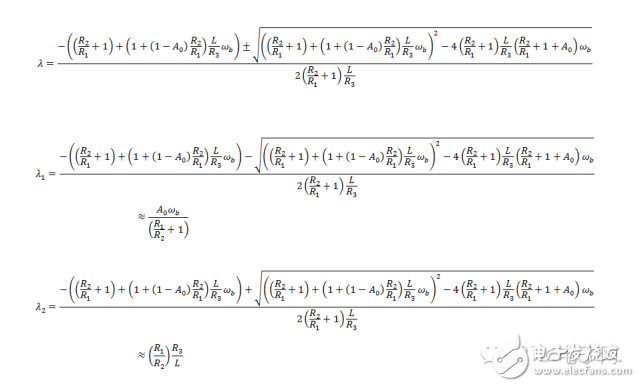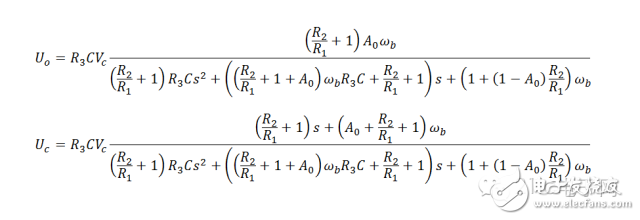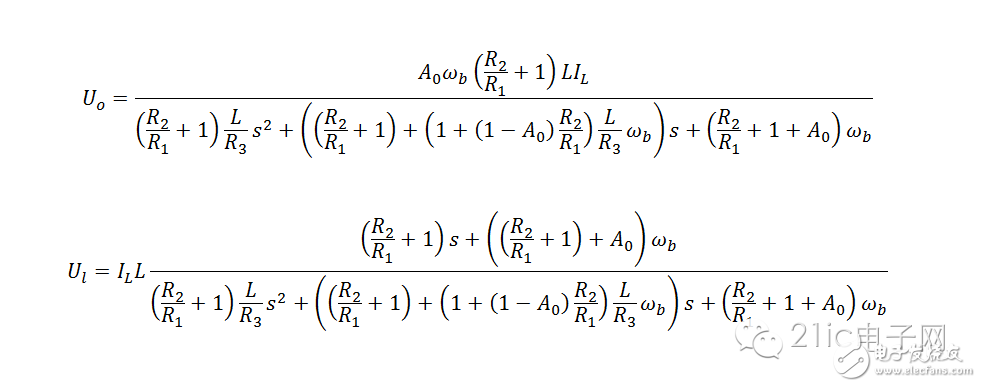给了个非常基础的思考题,但其却涉及到一些非常基本的概念。那题所涉知识非常基础(大学本科二年级),可惜却没人深入地分析一下。这里,给个详细分析,并引入另一个例子。
先引那个思考题帖:
http://bbs.21ic.com/icview-1623966-1-1.html上图先:
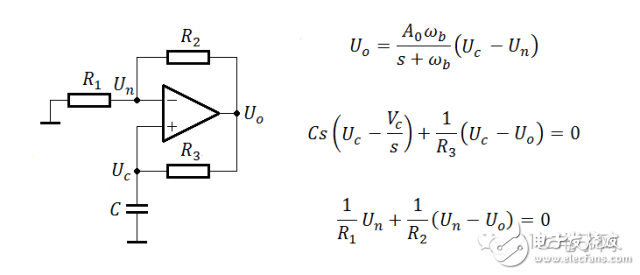
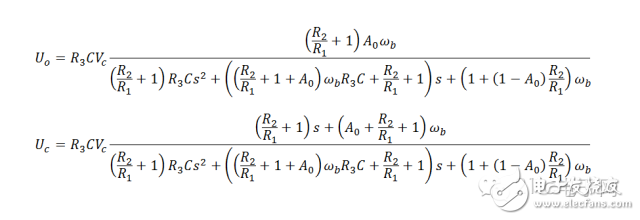 到此,可以说已经得到了“解”。不过,为了进一步分析,还得看看系统的特征根(极点)。见下式:
到此,可以说已经得到了“解”。不过,为了进一步分析,还得看看系统的特征根(极点)。见下式: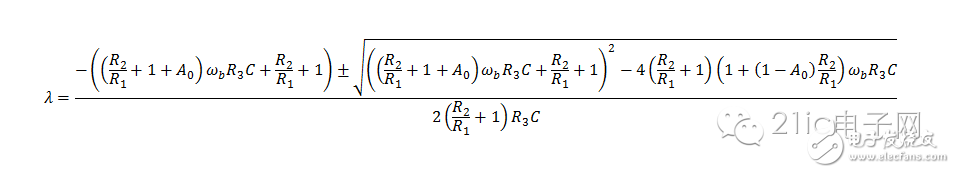
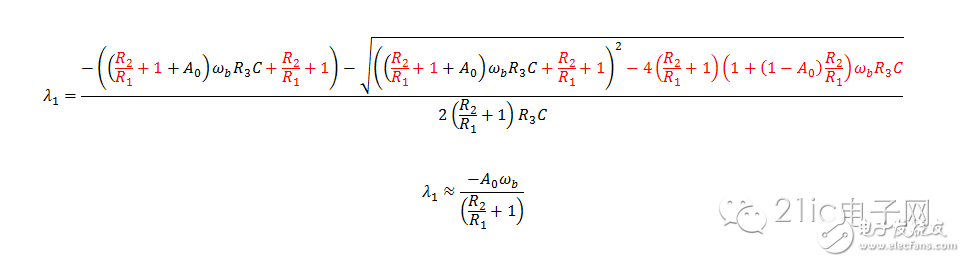
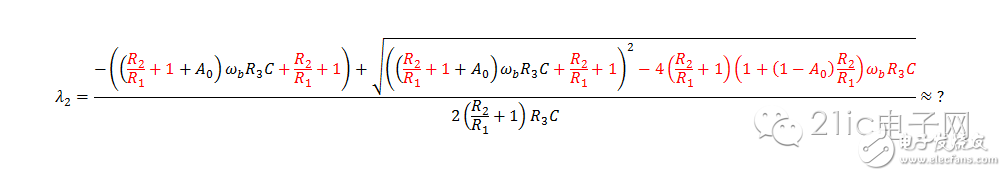 这个情况,如果将“红字”都忽略了则其结果是零,显然不太对。其实,这里是无穷大减无穷大,不定式!
这个情况,如果将“红字”都忽略了则其结果是零,显然不太对。其实,这里是无穷大减无穷大,不定式!换个玩法:
 这回奏效了!
这回奏效了!经过这么个极限近似,得到了两个特征根(极点):
 注意,上面那个有限,而下面那个趋于负无穷大。
注意,上面那个有限,而下面那个趋于负无穷大。现在,该确定移动轨迹的具体形态了。先给出部分分式分解,见下式:
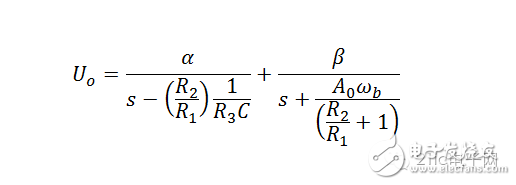
比对前式,有下列方程组,并解之:

注意到极限近似,有下式:
 至此,得到了我们需要的表达式:
至此,得到了我们需要的表达式: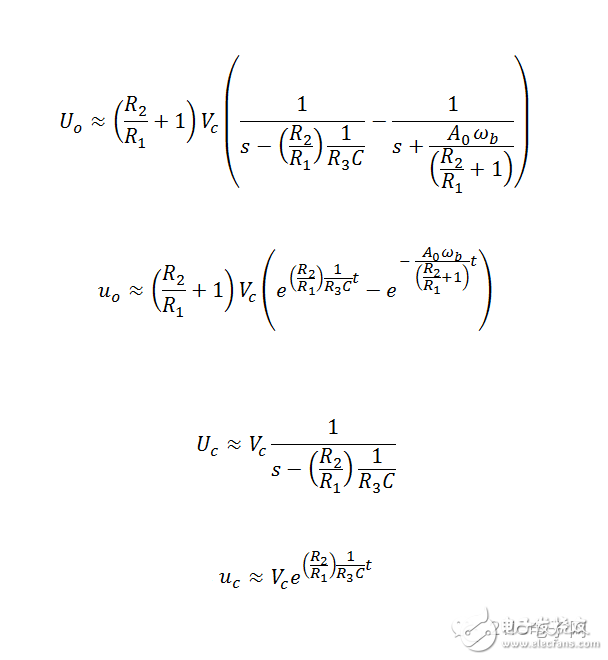
 上面,给的是参数(t)方程,下面给个直接的关系式:
上面,给的是参数(t)方程,下面给个直接的关系式: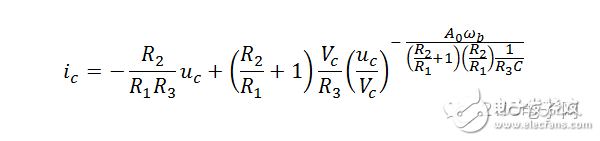 好了,到此该看看轨迹图了:
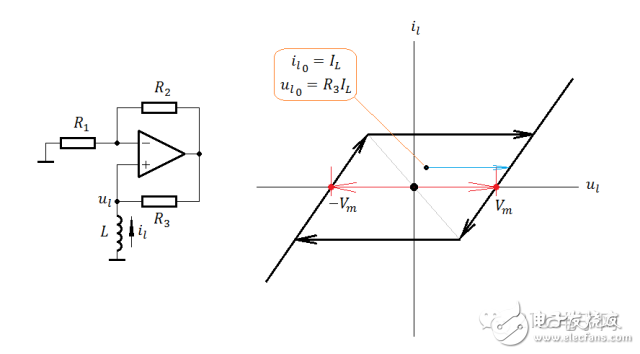
好了,到此该看看轨迹图了:图一
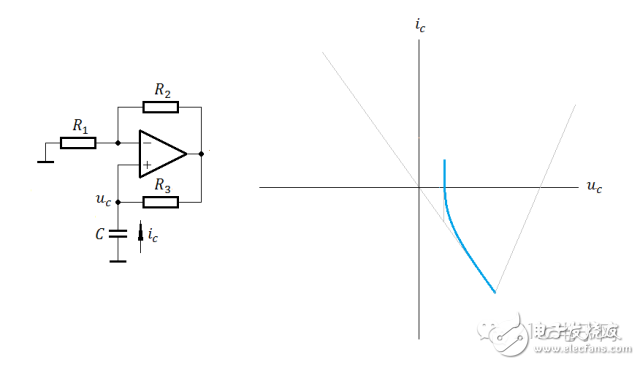
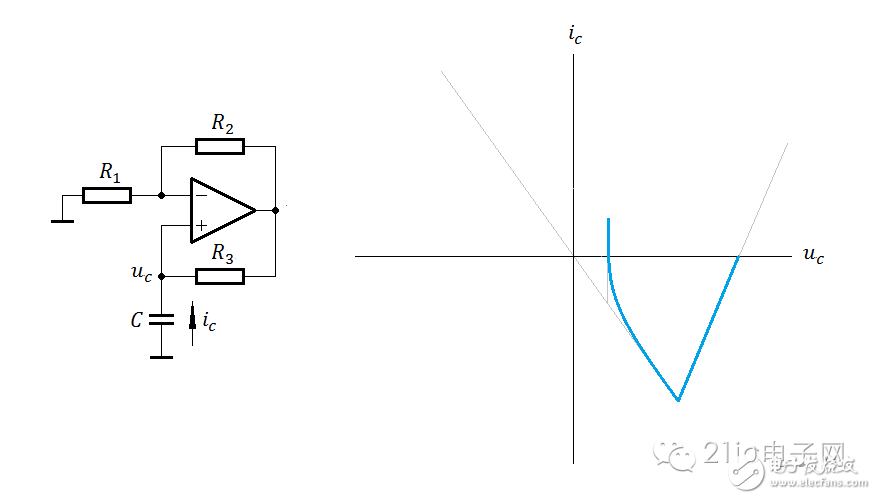
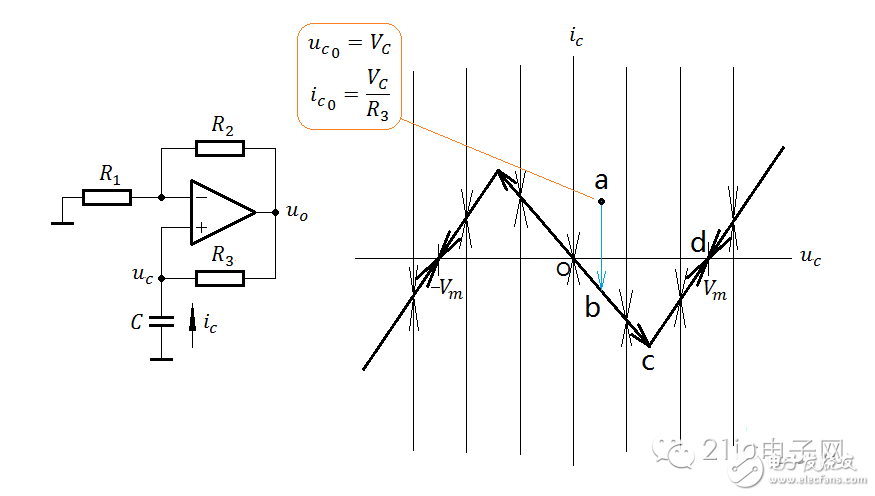 这图,给出了状态转移方向,是个非常全面且直观的轨迹图。可以任意设置一个初始点,然后画出其运动轨迹。
这图,给出了状态转移方向,是个非常全面且直观的轨迹图。可以任意设置一个初始点,然后画出其运动轨迹。补充几个式子,以说明限幅区段的具体情况:
 关于这个例子,说明几点:1)此例形象地展示了那个“负阻”,即稳定前提下的负阻轨迹。2)此例由任意非零初始点出发,将移动至两个状态终点之一,不可能振荡。3)负阻线(稳态)似乎有某种“引力”,可将原先不在其上的状态点瞬间吸引至负阻线上,前提是运放未被限幅。
关于这个例子,说明几点:1)此例形象地展示了那个“负阻”,即稳定前提下的负阻轨迹。2)此例由任意非零初始点出发,将移动至两个状态终点之一,不可能振荡。3)负阻线(稳态)似乎有某种“引力”,可将原先不在其上的状态点瞬间吸引至负阻线上,前提是运放未被限幅。下面,换个例子,见图:
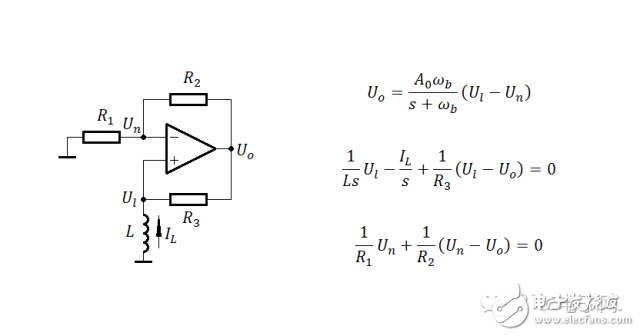

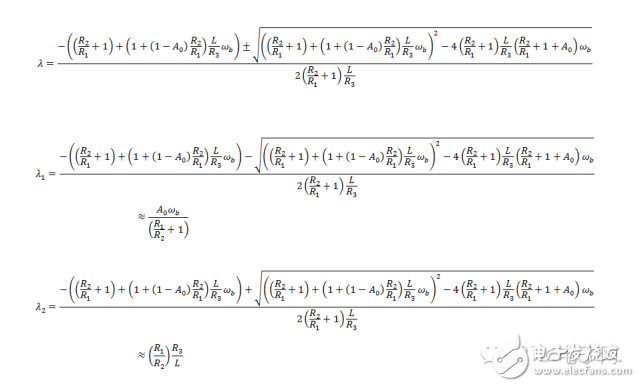 注意那个趋于正无穷大的特征根!
注意那个趋于正无穷大的特征根!相应的,给几个表达式:
 注意红线划的指数项。
注意红线划的指数项。给个关于第二例的轨迹图:
 由图可见,运放输入电压会高于限幅电压。
由图可见,运放输入电压会高于限幅电压。类似第一个例子,关于这个例子,说明几点:
1)此例说明,如果非稳定,根本就没有什么“负阻”,因为那条负阻轨迹线不存在。2)此例由任意非零初始点出发,将横向瞬间移动至左右两条限幅轨迹线之一,然后沿着轨迹线方向循环移动(即可以振荡)。3)原来的“负阻线”变成了非稳定平衡点所构成的线,其上的状态点(统计意义上说几率为零)在扰动下也将脱离此线移动至左或右。给出此帖的用意(包括那个思考题),就是让各位看看,《电路》(
电路分析、
电路原理或电路基础之类的)作为基础的重要性。虽然这里涉及到了非线性系统,但是作为最为简单的分段线性化分析,电路理论中的线性分析还是有其作用。当然,到了无法线性化的情况,那就必须运用纯粹的非线性分析,那是完全不同的一个领域。不过,如果连最为基本的线性分析都不会,却大谈非线性分析。可以肯定,那一定是忽悠!
所以,建议各位学生或初学者,认真踏实地学好《电路》。没那个基础,后续不可能有任何发展。当然,转行另论。 最后说明一下,其实“精确解”的形式前面早已经给出。第一个例子:
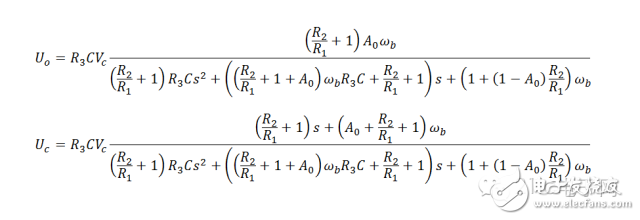 第二个例子:
第二个例子: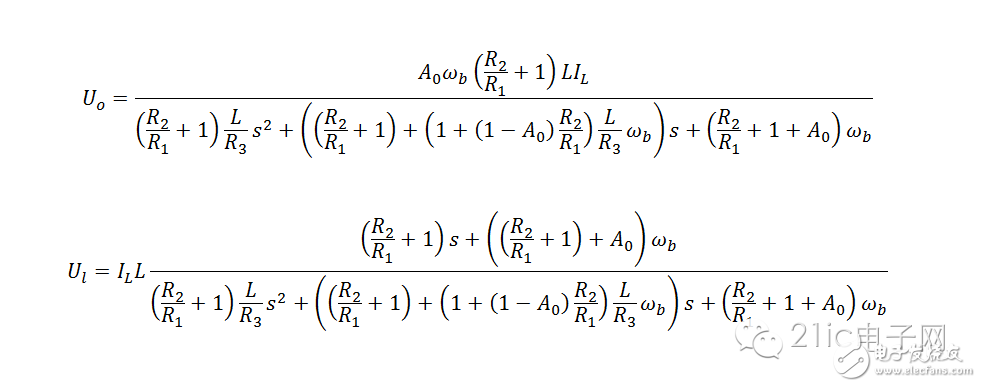 反馈是个动态过程,而动态模型起码是一阶。系统的动态特性在某些条件下可能隐而不显,譬如负反馈下的低频响应,但不是不存在。
反馈是个动态过程,而动态模型起码是一阶。系统的动态特性在某些条件下可能隐而不显,譬如负反馈下的低频响应,但不是不存在。

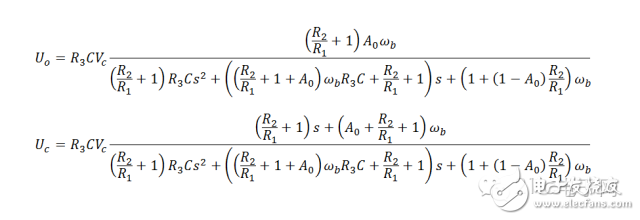
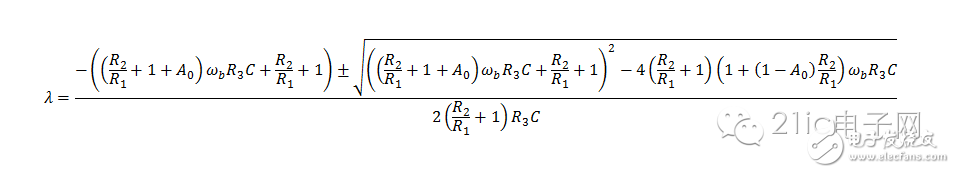
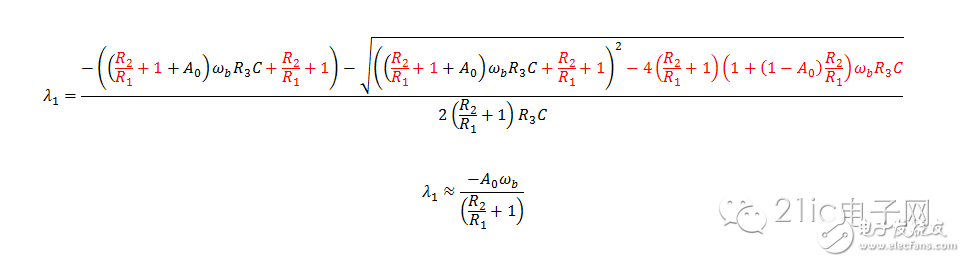
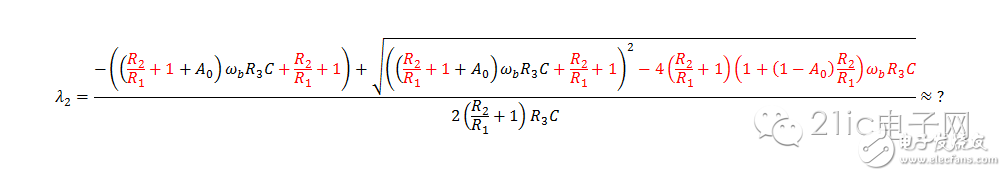


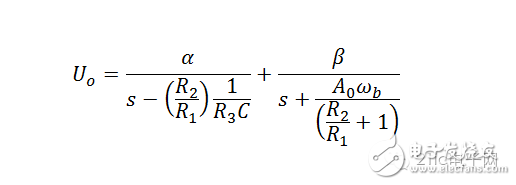

 至此,得到了我们需要的表达式:
至此,得到了我们需要的表达式: